(Szabados Tamás, 1997)

1.1 [Binomiális I] Adott n, p, D bemenő paraméterek esetén generáljon D darab független, n-edrendű p-paraméterű binomiális eloszlású véletlen számot. Egy ilyen véletlen számot úgy kaphat, ha megszámolja hogy n független kisérletből hányszor következik be egy p valószínűségű esemény. A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.2 [Binomiális II] Adott n, p, D bemenő paraméterek esetén generáljon D darab független, n-edrendű p-paraméterű binomiális eloszlású véletlen számot. Egy ilyen véletlen számot úgy kaphat, ha egy [0, 1)-en egyenletes eloszlású véletlen számot behelyettesít az eloszlásfüggvény "inverzébe" (Vetier 213. old.). A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.3 [Poisson I] Adott l , D bemenő paraméterek esetén generáljon D darab független, l -paraméterű Poisson eloszlású véletlen számot, a binomiális határeloszlásaként. Egy ilyen véletlen számot úgy kaphat, ha megszámolja hogy n független kisérletből hányszor következik be egy p valószínűségű esemény, ahol n kellően nagy és p kellően kicsi, úgy hogy np=l . A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.4 [Poisson II] Adott l , D bemenő paraméterek esetén generáljon D darab független, l -paraméterű Poisson eloszlású véletlen számot, exponenciális időtartamok leszámolásával (Deák 123. old.). Egy ilyen véletlen számot úgy kaphat, ha megszámolja, hogy hány egymás utáni l -paraméterű exponenciális időtartam fér bele az egységnyi hosszú időintervallumba. A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.5 [Poisson III] Adott l , D bemenő paraméterek esetén generáljon D darab független, l -paraméterű Poisson eloszlású véletlen számot, a binomiális határeloszlásaként. Egy ilyen véletlen számot úgy kaphat, ha egy [0, 1)-en egyenletes eloszlású véletlen számot behelyettesít az eloszlásfüggvény "inverzébe" (Vetier 213. old.). A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.6 [Negatív binomiális I] Adott k, p, D esetén generáljon D darab független, k-adrendű p-paraméterű negatív binomiális eloszlású véletlen számot. Egy ilyen véletlen számot úgy kaphatunk, ha megszámoljuk, hogy hányadik független kisérletre következik be k-adik alkalommal egy p valószínűségű esemény. A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.7 [Negatív binomiális II] Adott k, p, D esetén generáljon D darab független, k-adrendű p-paraméterű negatív binomiális eloszlású véletlen számot. Egy ilyen véletlen számot úgy kaphat, ha egy [0, 1)-en egyenletes eloszlású véletlen számot behelyettesít az eloszlásfüggvény "inverzébe" (Vetier 213. old.). A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.8 [Hipergeometrikus I] Adott K, M, n, D bemenő paraméterek esetén generáljon D darab független, n-edrendű, K, M paraméterű hipergeometrikus eloszlású véletlen számot. Egy ilyen számot úgy kaphat, ha megszámolja, hogy n elemű véletlen mintát véve (visszatevés nélkül) egy K darabból álló, M selejt darabot tartalmazó sokaságból, abban hány darab selejt lesz. A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.9 [Hipergeometrikus II] Adott K, M, n, D bemenő paraméterek esetén generáljon D darab független, n-edrendű, K, M paraméterű hipergeometrikus eloszlású véletlen számot. Egy ilyen számot úgy kaphat, ha egy [0, 1)-en egyenletes eloszlású véletlen számot behelyettesít az eloszlásfüggvény "inverzébe" (Vetier 213. old.). A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.10 [Normális I] Adott m, s , D bemenő paraméterek esetén generáljon D darab független, (m, s )-paraméterű normális eloszlású véletlen számot a centrális határeloszlás-tétel alapján (Deák 94. old.). Egy standard normális véletlen számot úgy kaphatunk, ha összeadunk 12 független, [0, 1]-en egyenletes eloszlású véletlen számot és az összegből levonunk 6-ot. Egy (m, s )-paraméterű normális eloszlású véletlen számot a standard-ből lineáris transzformációval nyerhetünk. A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.11 [Normális II] Adott m, s , D bemenő paraméterek esetén generáljon D darab független, (m, s )-paraméterű normális eloszlású véletlen számot polármódszerrel (Deák 96. old.). Két standard normális véletlen számot, x-et és y-t, úgy kaphatunk meg, ha veszünk két független, [0, 1]-en egyenletes eloszlású u és v véletlen számot, majd x = r cos z, y = r sin z, ahol Egy (m, s )-paraméterű normális eloszlású véletlen számot a standard-ből lineáris transzformációval nyerhetünk. A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.12 [Normális III] Adott m, s , D bemenő paraméterek esetén generáljon D darab független, (m, s )-paraméterű normális eloszlású véletlen számot módosított polármód-szerrel (Deák 98. old.). Két standard normális véletlen számot, x-et és y-t, a következő módon kaphatunk meg. Vegyünk két független, [0, 1]-en egyenletes eloszlású u1 és u2 véletlen számot, majd v1 = 2u1-1, v2 = 2u2-1, w = v12 + v22. Csak azokat az eseteket folytatjuk, ahol w£ 1 (csonkítás). Ekkor x = r v1 és y = r v2, ahol Egy (m, s )-paraméterű normális eloszlású véletlen számot a standard-ből lineáris transzformációval nyerhetünk. A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.13 [Exponenciális] Adott l , D bemenő paraméterek esetén generáljon D darab független, l -paraméterű exponenciális eloszlású véletlen számot eloszlástranszformáció-val. A kapott empirikus eloszlást hasonlítsa össze az elméletivel. Az eredményt grafikusan is szemléltesse.

1.14 [Gamma] Adott n, l , D bemenő paraméterek esetén generáljon D darab független, n-edrendű l -paraméterű gamma eloszlású véletlen számot. Egy ilyent n darab független exponenciális véletlen szám összeadásával kaphat, amelyeket viszont eloszlástranszformációval nyerhet. A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.15. [Cauchy] Adott D bemenő paraméter esetén generáljon D darab Cauchy-eloszlású véletlen számot eloszlástranszformációval. A kapott empirikus eloszlást hasonlítsa össze az elméletivel. Az eredményt grafikusan is szemléltesse.

1.16 [Polinomiális] Adott r<10 és n egész, p1>0, p2>0, ...,pr>0 (p1+p2+...+pr=1) valós bemenő adatok esetén generáljon r-dimenziós n-edrendű polinomiális eloszlású véletlen számokból D darabot (D is bemenő adat). Egy ilyen számot úgy kaphat, ha vesz n darab független, [0, 1]-en egyenletes eloszlású véletlen számot és megszámolja, hogy közülük hány darab esik a [0, p1), [p1, p1+p2), ... , [p1+...+pr-1, 1] intervallumokba. A kapott empirikus eloszlást hasonlítsa össze az elméletivel.

1.17 [Rendezett minta eloszlása] Adott n és k pozitív egész bemenő adatok esetén, ahol k£ n, generáljon n darab [0, 1)-en egyenletes eloszlású véletlen számot, és határozza meg közülük a nagyság szerinti k-adikat. Minket ennek a k-adik számnak az eloszlása érdekel. Ezt meghatározhatja közelítőleg úgy, hogy a fenti kisérletet D-szer elvégzi (D is bemenő adat), és meghatározza az empirikus eloszlást.

1.18 ["Tetszőleges" sűrűségfüggvényű eloszlás generálása szűréssel] Vegyen fel olyan f(x) sűrűségfüggvényeket, amelyek grafikonja valamely [a, b]´ [0, K] téglalapba esik. Ekkor úgy kaphat ilyen sűrűségfüggvényű véletlen számokat, ha generál a téglalapon egyenletes eloszlású (X, Y) számpárokat, de ezek közül csak azokat tartja meg, amelyekre X az f értelmezési tartományába esik és Y<f(X). Az így megszűrt X értékek sűrűségfüggvénye pontosan f lesz. Generáljon D darab ilyen véletlen számot (D bemenő adat) és hasonlítsa össze az empirikus eloszlást az elméletivel.

2.1 [Bolyongás koordinátája] Szabályos pénzérmével dobunk n-szer. Ha fej, akkor jobbra, ha írás, akkor balra lépünk egy-egy egységet a számegyenesen, így az Sn pontba jutunk. Ezt a kisérletet megismételjük D-szer. Határozza meg és szemléltesse a Sn tapasztalati eloszlását, illetve nagy n esetén Sn/Ö n tapasztalati eloszlását. (D és n bemenő paraméterek.)

2.2 [Bolyongás várakozási ideje ± n-ig] Szabályos pénzérmét dobálunk. Ha fej, akkor jobbra, ha írás, akkor balra lépünk egy-egy egységet a számegyenesen. Addig dobálunk, amíg vagy a +n pontba, vagy a -n pontba nem jutunk. Ehhez mondjuk t n lépés kellett. Ezt a kisérletet megismételjük D-szer. Határozza meg és szemléltesse t n tapasztalati eloszlását. (D és n bemenő paraméterek.)

2.3 [Bolyongás várakozási ideje a k-adik ± 2-ig] Szabályos pénzérmét dobálunk. Ha fej, akkor jobbra, ha írás, akkor balra lépünk egy-egy egységet a számegyenesen. Addig dobálunk, amíg az origótól 2 egység távol nem jutunk. Utána addig, amíg ettől a ponttól 2 egység távolra nem jutunk, és így tovább, összesen k-szor. Ehhez mondjuk t k lépés kellett. Ezt a kisérletet megismételjük D-szer. Határozza meg és szemléltesse t k tapasztalati eloszlását. (D és k bemenő paraméterek.)

2.4 [Bolyongás visszatérési ideje] Szabályos pénzérmét dobálunk. Ha fej, akkor jobbra, ha írás, akkor balra lépünk egy-egy egységet a számegyenesen. Addig dobálunk, amíg az origóba vissza nem jutunk. Ehhez mondjuk t lépés kellett. Ezt a kisérletet megismételjük nD-szer. Határozza meg és szemléltesse a t n kisérletből kapott átlagának tapasztalati eloszlását. (D és n bemenő paraméterek.)

2.5 [Bolyongás tartózkodási ideje a pozitív félegyenesen] Szabályos pénzérmével dobunk n-szer. Ha fej, akkor jobbra, ha írás, akkor balra lépünk egy-egy egységet a számegyenesen. Számolja meg, hogy az n lépésből összesen mennyi ideig tartózkodtunk az origótól jobbra, mondjuk t ideig. Ezt a kisérletet megismételjük D-szer. Határozza meg és szemléltesse a t n kisérletből kapott átlagának tapasztalati eloszlását. (D és n bemenő paraméterek.)

2.6 [Bolyongás tartózkodási ideje a pozitív félegyenesen a k-adik visszatérésig] Szabályos pénzérmével dobálunk. Ha fej, akkor jobbra, ha írás, akkor balra lépünk egy-egy egységet a számegyenesen. Addig dobálunk, amíg az origóba k-adszor is visszajutunk. Ehhez mondjuk t lépés kellett. Számolja meg, hogy az t lépésből relatíve mennyi ideig tartózkodtunk az origótól jobbra. Ezt a kisérletet megismételjük D-szer. Határozza meg és szemléltesse a relatív tartózkodási idő tapasztalati eloszlását. (D és k bemenő paraméterek.)

2.7 [Bolyongás maximuma] Szabályos pénzérmével dobunk n-szer. Ha fej, akkor jobbra, ha írás, akkor balra lépünk egy-egy egységet a számegyenesen. Határozza meg a bolyongás közben érintett legnagyobb x értéket, jelölje ezt Mn. Ezt a kisérletet megismételjük D-szer. Határozza meg és szemléltesse Mn tapasztalati eloszlását, illetve nagy n értékek esetén Mn/Ö n értékének tapasztalati eloszlását. (D és n bemenő paraméterek.)

2.8 [Bolyongás abszolút maximuma] Szabályos pénzérmével dobunk n-szer. Ha fej, akkor jobbra, ha írás, akkor balra lépünk egy-egy egységet a számegyenesen. Határozza meg az origótól való legnagyobb távolságot a bolyongás közben, jelölje ezt Mn. Ezt a kisérletet megismételjük D-szer. Határozza meg és szemléltesse Mn tapasztalati eloszlását, illetve nagy n értékek esetén Mn/Ö n értékének tapasztalati eloszlását. (D és n bemenő paraméterek.)

2.9 [Bolyongás visszatéréseinek száma] Szabályos pénzérmével dobunk n-szer. Ha fej, akkor jobbra, ha írás, akkor balra lépünk egy-egy egységet a számegyenesen. Határozza meg, hányszor tértünk vissza ezalatt az origóba, jelölje ezt a számot kn. Ezt a kisérletet megismételjük D-szer. Határozza meg és szemléltesse kn tapasztalati eloszlását, illetve nagy n értékek esetén kn/Ö n értékének tapasztalati eloszlását. (D és n bemenő paraméterek.)

2.10 [Bolyongás hullámhosszai] Szabályos pénzérmével dobunk n-szer. Ha fej, akkor jobbra, ha írás, akkor balra lépünk egy-egy egységet a számegyenesen. Hullámnak nevezzük az origóba való első visszatérésig tartó, illetve két visszatérés közötti részt. A kisérletet megismételve D-szer, határozza meg és szemléltesse a hullámhosszak tapasztalati eloszlását. (D és n bemenő paraméterek.)

2.11 [Bolyongás futamai] Szabályos pénzérmével dobunk n-szer. Ha fej, akkor jobbra, ha írás, akkor balra lépünk egy-egy egységet a számegyenesen. Futamnak nevezünk két írás közötti tiszta fej sorozatot (monoton jobbra tartó részsorozatot). A kisérletet megismételve D-szer, határozza meg és szemléltesse a futamok hosszának tapasztalati eloszlását. (D és n bemenő paraméterek.)

2.12 [Van-e memóriája a bolyongásnak?] Szabályos pénzérmével dobunk n-szer. Ha fej, akkor jobbra, ha írás, akkor balra lépünk egy-egy egységet a számegyenesen. Megvizsgáljuk, hogy k darab egymásutáni fej után (k<10) milyen valószínűséggel dobtunk még egy fejet. A kisérletet megismételve D-szer, határozza meg és szemléltesse a fej feltételes relatív gyakoriságát a k függvényében. Sok egymás utáni fej után kisebb valószínűséggel fogunk még egy fejet dobni? (D és n bemenő paraméterek.)

2.13 [Bolyongás, tiszta fejek] Szabályos pénzérmével dobunk n-szer. Ha fej, akkor jobbra, ha írás, akkor balra lépünk egy-egy egységet a számegyenesen. Határozza meg a leghosszabb egymás utáni tiszta fej részsorozat (monoton jobbra tartó részsorozat) hosszát, jelölje ezt a számot kn. Ezt a kisérletet megismételjük D-szer. Határozza meg és szemléltesse kn tapasztalati eloszlását, illetve nagy n értékek esetén kn/log2n tapasztalati eloszlását. (D és n bemenő paraméterek.)

2.14 [Bolyongás falba ütközésig] Szabályos pénzérmével dobálunk. Ha fej, akkor felfelé, ha írás, akkor lefelé lépünk egy-egy egységet a függőlegesen elhelyezett x-tengelyen. Képzelje el a bolyongás grafikonját a t idő függvényében (a t-tengely vízszintes). Addig bolyongunk, amíg bele nem ütközünk egy előre meghatározott falba. Az ütközéskor csak az x-koordináta eloszlása érdekel bennünket. Határozza meg ezt közelítőleg, D-szer eljutva az ütközésig. Két esetet vizsgáljon meg:

(a) A fal egyenlete (R bemenő adat).

(b) A fal egyenlete 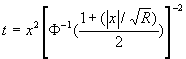, ahol R bemenő adat és F -1 a standard normális eloszlás eloszlásfüggvényének inverze, amit pl. táblázatból lehet a gépbe bevinni.

2.15 [Kétdimenziós bolyongás pályája] Két szabályos pénzérmével dobunk n-szer. Ha az első érme fej, akkor jobbra, ha írás, akkor balra lépünk egy egységet. Ha a második érme fej, akkor felfelé, ha írás, akkor lefelé lépünk egy egységet. Így az n-edik dobás után az (Sn, Tn) pontba jutunk. Szemléltesse a bolyongás pályáját a síkon. Ezt a kisérletet megismételjük D-szer. Határozza meg külön-külön az Sn és Tn koordináták tapasztalati eloszlását. Szemléltesse a két koordináta együttes tapasztalati eloszlását a síkon. (D és n bemenő paraméterek.)

3. Játékok

3.1 [Pétervári játék.] A játékos F forintot fizet a banknak. Ezért addig dobálhat egy szabályos pénzérmét, amíg fej nem lesz. Ha a k-adik kisérletre jött ki az első fej, akkor a játékos 2k forintot kap a banktól. Ezt a kisérletet nD-szer végrehajtva vizsgálja meg a játékos n játék alatti átlagos nyereségének eloszlását. Lehet-e úgy megválasztani F értékét, hogy a játék igazságos legyen, azaz az átlagos nettó nyereség akármilyen nagy n esetén 0 körül ingadozzék? Ossza el az n játék alatti átlagos nyereséget log2n-nel és így is nézze meg az eloszlást, ha n nagy. (D és n bemenő paraméterek.)

3.2 [Game of craps.] A játékos két kockával dob és a dobott számok összege számít. Ha az első dobás 7 vagy 11, akkor rögtön nyer. Ha a dobás 2,3, vagy 12, akkor rögtön veszít. Egyébként, ha a dobás 4,5,6,8,9,10, akkor ennyi lesz a játékos pontja és folytatnia kell a dobálást. Addig dob, amíg vagy megdobja a pontját, vagy pedig 7-et dob. Az első esetben nyer, az utóbbi esetben veszít. Szimulálja a játékot és határozza meg a nyerés relatív gyakoriságát. Hasonlítsa ezt össze az elméletileg várttal.

3.3 [Buffon-féle tűprobléma.] Szimulálja a tűdobálós játékot (tankönyv 504. old.) D-szer. Hasonlítsa össze a kapott eredményt az elméletileg várttal különféle D értékekre.

3.4 [Gyufadobálás.] Szimulálja a gyufadobálást négyzethálós papírra (tankönyv 508. old.) D-szer. Hasonlítsa össze a kapott eredményt az elméletileg várttal különféle D értékekre.

3.5 [De Mére lovag kérdése] Dobjunk fel egy kockát 4-szer. Ezt ismételjük meg D-szer. Nézzük meg annak a relatív gyakoriságát, hogy volt legalább egy hatos. Utána dobjunk fel két kockát 24-szer és ezt is ismételjük meg D-szer. Most annak a relatív gyakoriságát nézzük, hogy volt dupla hatos. Hasonlítsuk össze a két relatív gyakoriságot egymással és az elméletileg várttal. (D bemenő adat.)

3.6 [Rulett tétduplázással] Felteszünk egy zsetont a pirosra. (A piros 18/37 valószínűséggel jön ki és a tét dupláját fizeti.) Ha nyerünk, abbahagyjuk a játékot. Ha veszítünk, akkor 2 zsetont teszünk a pirosra. Ha nyerünk, abbahagyjuk a játékot. Ha veszítünk, akkor 4 zsetont teszünk a pirosra. Addig folytatjuk vesztés esetén a tétduplázást, amíg nem fogy el a J kezdő tőkénk. (J bemenő adat.) Ezt a kisérletet D-szer megismételve vizsgálja meg, hogy tudunk-e ezzel a stratégiával átlagban nyerni. (D is bemenő adat.)

3.7 [Rulett minimális kockázattal] Csak egyetlen zsetont veszünk. Feltesszük ezt a pirosra. (A piros 18/37 valószínűséggel jön ki és a tét dupláját fizeti.) Ha vesztünk, abbahagyjuk a játékot. Ha nyerünk, akkor most meglévő 2 zsetonunkat a piroson hagyjuk. Ha vesztünk, abbahagyjuk a játékot. Ha nyerünk, akkor a most meglévő 4 zsetonunkat hagyjuk a piroson. Addig folytatjuk nyerés esetén a tétduplázást, amíg el nem érjük a célként kijelölt J pénzmennyiséget. (J bemenő adat.) Ezt a kisérletet D-szer megismételve vizsgálja meg, hogy tudunk-e ezzel a stratégiával átlagban nyerni. (D is bemenő adat.)

3.8 [Tönkremenés.] Egy játékos a bank ellen játszik. Minden játékban, a többitől függetlenül, adott p valószínűséggel nyer (0<p<1) és q=1-p valószínűséggel veszít. Induláskor a játékosnak J, a banknak B tőkéje van. A játék addig folyik, míg vagy a játékos, vagy a bank tönkre nem megy, legyen ez az idő t . Közelítőleg határozza meg és szemléltesse t eloszlását illetve a játékos tönkremenetelének valószínűségét különféle J és B bemenő paraméterek mellett.

3.9 [Ping-pong.] Szimulálja a ping-pong játékot (tankönyv 459. old.) adott állásból indulva D-szer. Hasonlítsa össze az eredményt az elméletileg várttal, különféle D-ek esetén. (Az állás és D bemenő paraméterek.)

3.10 [Dart dobálás.] Szimulálja azt a játékot, hogy n darab kis nyilat dobálunk egy céltáblára D-szer. A táblán koncentrikus körök vannak, különféle pontértékekkel. Hasonlítsa össze a nyilak tapasztalati eloszlását az elméletileg várttal különféle n és D bemenő paraméterekre.

3.11 [Póker.] Szimuláljon 5 lapos póker-leosztásokat, 52 lapos francia kártyából. Határozza meg a különféle neves leosztások relatív gyakoriságát: egy pár, két pár, hármas, sor (straight), szín (flush), hármas+pár (full), négyes (poker), sor+szín (straight flush) és sor+szín ásszal (royal flush), és hasonlítsa össze az elméletileg várttal.

3.12 [Kecske vagy kocsi?] Egy TV-showban a nyertes három ajtó közül választhat. Két ajtó mögött kecske van, a harmadik mögött pedig egy autó. Amikor a győztes ráteszi kezét az egyik kilincsre, a műsorvezető megállítja, kinyitja a másik két ajtó egyikét, és megmutatja, hogy amögött kecske van. Igaz-e, hogy emiatt 1/3-ról 1/2-re nő a versenyző esélye, hogy az elsőként kiválasztott ajtó mögött a kocsi lesz? Vizsgálja meg szimulációval a következő két esetet:

- a műsorvezető tudja, hogy hol az autó, és persze nem azt az ajtót nyitja ki,

- a műsorvezető sem tudja, hogy hol az autó, de véletlenül olyan ajtót nyit ki, amely mögött kecske van.

Ezután a műsorvezető felteszi a kérdést, hogy a versenyző akarja-e inkább a másik, ki nem nyitott ajtót megnézni. Szimulációval döntse el, hogy javít-e az esélyen az a stratégia, ha a versenyző ilyenkor igennel válaszol.

3.13 [Van-e nyerő stratégia a lottón?] Próbáljon kitalálni valamilyen előnyösnek tűnő stratégiát a lottón és szimulációval ellenőrizze, hogy beválik-e.

4.1 [Bertrand-paradoxon I.] Képernyőn szimulálja a Bertrand-paradoxon (a) változatát (tankönyv 512. old.) D-szer. Hasonlítsa össze az eredményt az elméletileg várttal különféle D bemenő paraméterekre.

4.2 [Bertrand-paradoxon II.] Képernyőn szimulálja a Bertrand-paradoxon (b) változatát (tankönyv 512. old.) D-szer. Hasonlítsa össze az eredményt az elméletileg várttal különféle D bemenő paraméterekre.

4.3 [Bertrand-paradoxon III.] Képernyőn szimulálja a Bertrand-paradoxon (c) változatát (tankönyv 512. old.) D-szer. Hasonlítsa össze az eredményt az elméletileg várttal különféle D bemenő paraméterekre.

4.4 [Terület-becslés.] Az x2+k2y2£ 1 (k³ 1) ellipszis (vagy más korlátos síkidom) területét megbecsülhetjük úgy, hogy független, egyenletes eloszlású véletlen pontokat dobunk le az ellipszist befoglaló négyzetre és meghatározzuk annak a relatív gyakoriságát, hogy egy (x,y) pont az ellipszis belsejébe esik, azaz fennáll rá az ellipszist meghatározó egyenlőtlenség. Vesse össze az így kapott közelítést az elméletileg várt területtel. Mi történik, amikor az ellipszis nagyon keskeny? (A kisérletek száma, D, és a k paraméter bemenő adat.)

4.5 [Levelek és borítékok.] Egy felületes titkárnő a munkanapja végén teljesen véletlenszerűen teszi borítékokba az aznap megírt n darab levelet. Mi a valószínűsége, hogy egy levél sem kerül a helyére? Szimulálja ezt D-szer és hasonlítsa össze az eredményt az elméletileg várttal, különféle n és D bemenő értékek mellett.

4.6 [Szinbád.] Szimulálja a Szinbád-féle feleség-választási M-stratégiát (tankönyv 500. old.) számítógépen D-szer. Hasonlítsa össze az eredményt az elméletileg várttal különféle M és D bemenő paraméterekre.

4.7 [Születésnap.] Egy teremben n ember van. Kisérletekkel vizsgálja meg annak az eseménynek a relatív gyakoriságát az n függvényében, hogy van köztük legalább kettő, akinek azonos a születésnapja (kizárólag 365 napos évet véve). Hasonlítsa össze az eredményt az elméletileg várttal. (Az n értéke és a kisérletek D száma bemenő adat.)

4.8 [Nagy számok törvénye I] Átlagoljon k darab (k=1,2,...,n) [0,1]-en egyenletes eloszlású, független véletlen számot. Minden egyes k-ra ezt a kisérletet végezze el D-szer és szemléltesse a kapott eloszlást hisztogrammal. (D és n bemenő adat.)

4.9 [Nagy számok törvénye II] Átlagoljon k darab (k=1,2,...,n) Cauchy eloszlású, független véletlen számot, amelyeket egyenként eloszlástranszformációval kaphat. Min-den egyes k-ra ezt a kisérletet végezze el D-szer és szemléltesse a kapott eloszlást hisztogrammal. (D és n bemenő adat.)

4.10 [Centrális határeloszlás-tétel.] Adjon össze k darab (k=1,2,...,n) [0,1]-en egyenletes eloszlású, független véletlen számot és standardizálja az összeget. Minden egyes k-ra ezt a kisérletet végezze el D-szer és szemléltesse a kapott eloszlást hisztogrammal. Hasonlítsa össze az eredményeket a standard normális eloszlással. (D és k bemenő adat.)

4.11 [Vonat] Adott n számú utas véletlenszerűen (egymástól függetlenül, azonos valószínűséggel) száll fel r darab vasúti kocsira (r<10). Ezt D-szer megismételve, határozza meg a vasúti kocsikban lévő utasok számának empirikus eloszlását. Melyik elhelyezkedés a leggyakoribb? (D, r és n bemenő adat.)

4.12 [A standard normális eloszlásfüggvény és inverzének táblázata] Készítsen tetszőleges módszerrel (pl. numerikus integrálással vagy empirikus eloszlásfüggvénnyel való közelítéssel) a standard normális F eloszlásfüggvényt kiszámítani tudó függvényeljárást. Ennek segítségével, adott y (0<y<1) értékek esetén oldja meg a F (x)=y egyenletet pl. Newton-módszerrel. Így készíthet a F inverzéről is táblázatot.

4.13 [A c 2 eloszlás táblázata] Adott n pozitív egész bemenő adat esetén adja össze n darab standard normális eloszlású véletlen szám négyzetét. Ekkor a kapott szám n-szabadságfokú c 2 eloszlású lesz. Ezt ismételje meg D-szer (D is bemenő adat), és így készítsen egy (empirikus) eloszlásfüggvény táblázatot.

5.1 [Jótündér.] Szimulálja a Jótündér vérében lejátszódó vírus-szaporodási folyamatot különféle p paraméterek esetén n másodpercig (tankönyv 469. old., n és p bemenő adat). Hasonlítsa össze a kapott eredményeket az elméletileg várt valószínűségekkel, vagy azzal, hogy elméletileg mennyi a vírusok várható száma n másodperc után.

5.2 [Rádióaktív bomlás I.] D atom van, amelyek mindegyike a többitől függetlenül, spontán, adott l -paraméterű exponenciális eloszlású várakozási idő után elbomlik. Szimulálja a t idő függvényében (t<T) a megmaradt atomok számát, és hasonlítsa össze az elméletileg várt exponenciális bomlási törvénnyel. (D, T és l bemenő adat.)

5.3 [Rádióaktív bomlás II.] Az idő diszkrét időegységekben múlik. D atom van, amelyek mindegyike a többitől függetlenül, spontán, bármely diszkrét időpontban adott p valószínűséggel elbomlik (0<p<1). Szimulálja a t idő függvényében (t<T) a megmaradt atomok számát, és hasonlítsa össze az elméletileg várt exponenciális bomlási törvénnyel. (D, T és p bemenő adat.)

5.4 [Taxi.] Szimulálja a taxira várakozás folyamatát (tankönyv 457. old.). Hasonlítsa össze az eredményt az elméletileg várttal.

5.5 [Kiszolgálás.] Egy kis élelmiszerüzletben egyetlen eladónő dolgozik. Az egyes vásárlók érkezése között l -paraméterű exponenciális eloszlású véletlen várakozási idő van. Egy vásárló kiszolgásának ideje t -paraméterű exponenciális eloszlású véletlen időtartam. A véletlen időtartamok mind függetlenek. A sorban legfeljebb 10-en állnak, mert aki 11-ediknek érkezik, az elmegy vásárlás nélkül. Szimulálja ezt a kiszolgálási folyamatot. (A l , t paraméterek és a szimuláció T ideje bemenő adat.)

5.6 [Lift.] Szimulálja egy 10 emeletes ház négyszemélyes liftjének működését. A földszinten érkező és az i-edik (i=1,...,10) emeletre tartó bármely két ember érkezése között l -paraméterű exponenciális eloszlású véletlen időtartam van. Az egyes emeletekről lefelé igyekvők érkezése között ugyancsak. A véletlen időtartamok mind függetlenek. (Tehát a földszinten átlagosan 10-szer annyi ember érkezik, mint egyetlen emeleten. A földszinten érkező emberek meg vannak jelölve aszerint, hogy melyik emeletre igyekeznek.) A földszinten legfeljebb 8-an, az emeleteken legfeljebb 4-en állnak sorban, mert a többiek elindulnak gyalog a lépcsőn. Az egyszerűség kedvéért az emeletekről mindenki csak a földszintre igyekszik. A lefelé tartók csak akkor szállnak be, ha a lift lefelé halad. A lift felfelé mindenütt megáll, ahol valaki ki akar szállni. Ha a lift kiürült, akkor felmegy a legmagasabb olyan emeletre, ahol van beszálló. Lefelé mindenütt megáll, ahol valaki be akar szállni, feltéve, hogy még nincs tele. Ha a lift kiürül, és nincs hívás, akkor azon a szinten vár, ahol kiürült. A lift sebességét vegye c sec/emelet-nek. A ki-beszálláshoz szükséges időt vegye c sec-nak. (A l , c paraméterek és a szimuláció T ideje bemenő adat.)