Tesztfeladat az utazóügynök problémához

Gráfok tárolása szomszédsági mátrixszal
1.feladat
Gráf izomorfia
2. feladat
Utazó ügynök probléma
Brute froce
Karp-Held algoritmussal

Gráfok tárolása szomszédsági mátrixszal

Egy egyszerű (nincs többszörös vagy hurok éle) G gráf szomszédsági mátrixa egy 0-1 mátrix, melyben az (i,j) elem 1, ha van él az i-edik és j-edik csúcs között, 0 ha nincs. Ha a G gráf súlyozott, akkor a szomszédsági mátrixban az egyesek helyére az élsúlyokat írjunk.

1.feladat

Mikor lesz a szomszédsági mátrix szimmetrikus?
Igazoljuk, hogy A^k (i,j)-edik eleme az i-edik csúcsból a j-edik csúcsba menő pontosan k hosszú utak száma (nem feltétlen egyszerű utak).
Hogyan lehetne a hatványok segítségével eldönteni, hogy G összefüggő-e?

Gráf izomorfia

Két számozott csúcsokkal rendelkező gráfot izomorfnak nevezünk, ha az egyik gráf előállítható a másik csúcsainak átszámozásával. Megmondani két gráfról, hogy izomorfak-e nem könnyű feladat. Ha viszont adott egy gráf (például az A szomszédsági mátrixával) és egy permutáció, amellyel át akarom számozni a csúcsokat, akkor ki tudjuk számítani az új gráf szomszédsági mátrixát. Tegyük fel, hogy az 1,2,...,n csúcsokat szeretném átszámozni a 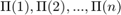$\Pi(1), \Pi(2),...,\Pi(n)$ permutációval. Készítsünk el két mátrixot, amely csupa 0-ből és 1-ből áll, és összesen n darab 1-est tartalmaz. A P1 mátrixban a k-dik sorban a 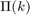$\Pi(k)$ -dik pozícióban legyen az 1-es, a P2 mátrixban az m-dik oszlopban a 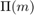$\Pi(m)$ -dikben.

2. feladat

Gondoljuk meg, hogy ekkor P1 és P2 is minden oszlopban és minden sorban pontosan egy darab 1-est tartalmaz.
Igazoljuk, hogy 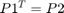és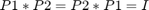
Bizonyítsuk be, hogy a 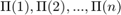$\Pi(1), \Pi(2),...,\Pi(n)$ sorrendben felírva a csúcsokat a gráf szomszédsági mátrixa 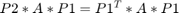lesz.

Utazó ügynök probléma

3. feladat Készítsünk saját tesztfeladatot az utazó ügynök problémához! Legyen skálázható (akárhány városra gyorsan kiszámítható legyen a szomszédsági mátrix). Aztán teszteljük, hogy az alábbi algoritmusok hány városig tudják megoldani a feladatot! Legyen a kapott szomszédsági mátrix a G, ekkor a tic, toc segítségével mérhetünk futásidőt.

Brute froce

function minham=tsbf(A)

n=length(A); 
p=perms(1:n);
minham=sum(sum(A));

for i=1:size(p,1)
    h=0;
    for j=1:n-1
    h=h+A(p(i,j),p(i,j+1));
    end
    h=h+A(p(i,end),p(i,1));
    if h<minham
        minham=h; 
    end
end

Karp-Held algoritmussal

function minham=tsdp(A)

minham=tsdpr(2:length(A),1,A);  

function y=tsdpr(S,l,A)
 
if length(S)==1 
    y=A(l,S)+A(S,1); 
else 
    hossz=zeros(length(S),1);
     for m=1:length(S) 
        hossz(m)=tsdpr(S([1:m-1, m+1:end]),S(m),A)+A(S(m),l);
     end
     y=min(hossz);
end