Gyakorlat -- Sage

Sage gyakorlat

Kezelőfelület:

sor végi ENTER -> új sort kezd
SHIFT ENTER -> végrehatja az adott cellát
Escape -> futtatás megszakítása
ctrl ; -> az adott cellát szétvágja két részre
ctrl ENTER -> az adott cellát szétvágja két részre, és futtatja mindkét darabot
ctrl BACKSPACE -> az adott cellát összevonja az előző cellával
alt ENTER -> Futtatj a cellát, majd utána új mezőt nyit
a kék csíkra kattintva lehet egérrel új mezőt nyitni (ha közben a SHIFT-et lenyomva tartjuk, akkor olyan megjegyzést írhatunk, mint ez is)
a megjegyzézeket dupla kattintással tudjuk megint szerkeszthetővé tenni
ha cellán belül egy vagy több sorban kijelölünk részeket (a SHIFT és a nyilak segítségével vagy egérrel), akkor Firefoxban a TAB és SHIFT+TAB hatására változtathatjuk a kijelölt sorok behúzását
A eredmények előtt van egy kis fehér rész, ami felett az egér kézzé alakulva jelzi, hogy funkciója van. 3 állapot között lehet váltani: az eredmény normál megjelenítése, egy sorban való kiíratása, vagy az eredmény eltüntetése.
Van lehetőség LaTeX kódok írására megjegyzések között:
∫0∞sin(x)/x=2π

Segítség a parancsokhoz:

help(parancs) + SHIFT ENTER -> egy linket ad, amivel új oldalon nyílik meg a parancs leírása
parancs? + SHIFT ENTER -> a parancs leírása
parancs? + TAB -> a parancs leírását csak megmutatja
paran +TAB -> kiegészíti a parancs nevét, illetve ha ez nem egyértelmű, akkor megadja az opciókat. Az opciók közül nyilakkal választhatunk. Ha ekkor az egyik opción nyomunk mégegy TAB-ot, akkor kiírja a hozzá tartozó leírást.

randint(1,2)

szamok=[] while len(szamok) < 5: x = randint(1,90) if not x in szamok: szamok = szamok + [x] szamok

[69, 59, 88, 45, 15]

sorted(szamok)

[15, 45, 59, 69, 88]

Régóta megoldatlan sejtés, hogy a következő szabályok ismétlésével minden egész számból indítva el az 1-hez jutunk:

- ha a szám páros, akkor osszuk el 2-vel

- ha a szám páratlan, akkor szorozzuk meg 3-mal és adjunk hozzá egyet.

Írjunk egy harom(n) nevű függvényt, amely egy listában visszaadja a megtett lépéseket egészen 1-ig.

def harom(n): l = [n] while n!=1: if n%2 == 0: n = n/2 else: n = 3*n+1 l.append(n) return l

harom(7)

[7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1]

def csupanullaegy(n): if n%10>1: return False elif n > 10: return csupanullaegy(n//10) else: return True

csupanullaegy(1001)

True

def csupanullaegytobbszoros(n): t=n while not(csupanullaegy(t)): t=t+n return t

csupanullaegytobbszoros(87)

11010111

Az all parancs egy listát kér paraméterként és akkor tér vissza True-val, ha a kapott lista minden eleme logikailag igaz, egyébként False eredményt ad.

all([True,True])

True

all([True,False,True])

False

Az any parancs akkor ad vissza True értékkel, ha a paraméterként adott lista legalább egyik eleme True, különben False értéket ad vissza.

any([False,False,True])

True

A str(123) eredménye '123' lesz. A stringen a for ciklus karakterenként megy végig:

for c in str(123): print c

1
2
3

A csupanullaegy(n) függvény rövidebb megírása (True-val tér vissza, ha n minden számjegye 0 vagy 1):

def csupanullaegy(n): return all([c in ['0','1'] for c in str(n)])

csupanullaegy(101)

True

csupanullaegy(121)

False

A permutations(l) az l listának az összes lehetséges permutációit adja vissza.

A combinations(l,k) az l lista összes k-asával tér vissza.

permutations(range(4))

[[0, 1, 2, 3], [0, 1, 3, 2], [0, 2, 1, 3], [0, 2, 3, 1], [0, 3, 1,
2], [0, 3, 2, 1], [1, 0, 2, 3], [1, 0, 3, 2], [1, 2, 0, 3], [1, 2,
3, 0], [1, 3, 0, 2], [1, 3, 2, 0], [2, 0, 1, 3], [2, 0, 3, 1], [2,
1, 0, 3], [2, 1, 3, 0], [2, 3, 0, 1], [2, 3, 1, 0], [3, 0, 1, 2],
[3, 0, 2, 1], [3, 1, 0, 2], [3, 1, 2, 0], [3, 2, 0, 1], [3, 2, 1,
0]]

combinations(range(6),3)

[[0, 1, 2], [0, 1, 3], [0, 1, 4], [0, 1, 5], [0, 2, 3], [0, 2, 4],
[0, 2, 5], [0, 3, 4], [0, 3, 5], [0, 4, 5], [1, 2, 3], [1, 2, 4],
[1, 2, 5], [1, 3, 4], [1, 3, 5], [1, 4, 5], [2, 3, 4], [2, 3, 5],
[2, 4, 5], [3, 4, 5]]

A nyolc királynő problémát szeretnénk megoldani rövidebb kóddal, mint az elődáson tettük. Ehhez tekintsük a range(8) lista permutációit, például az x=[6,3,4,1,5,2,7,0] elemet. Ehhez az x-hez rendeljünk hozzá a bábuk egy állását: az i-edik oszlopban lévő királynőt tegyük az x[i]-edik sorba. Természetesen most a sorokat és az oszlopokat is 0-tól kezdjük sorszámozni.

Szeretnénk meghatározni a királynők összes jó lepakolását. Mindegyik oszlopban egy királynő lesz (az i. oszlopban az x[i]. sorban), így az oszlopok rendben lesznek. Egy soron belül sem lehet két királynő, mivel a [0,1,2,3,4,5,6,7] halmaz egy permutációját nézzük. Már csak az átlók helyességét kell megnéznünk.

Két királynő átlóban akkor üti egymást, ha az oszlopuk sorszámának abszolútértékes különbsége megegyezik a soraik sorszámának abszolútértékes különbségével. Ezt egyszerűen tudjuk ellenőrizni: i-vel és j-vel is végigmegyünk az összes oszlopon (ez összesen 8*8=64 lehetőség), és ha abs(i-j) != abs(x[i]-x[j]), akkor az i. és j. oszlopban lévő királynők nem ütik egymást.

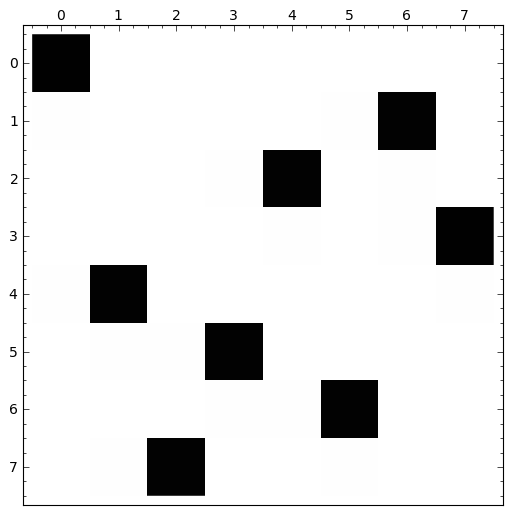
Arra kell még figyelnünk, hogy i==j esetén nincs mit vizsgálnunk az átlókkal kapcsolatban. Azon eseteket íratjuk ki, ahol az összes i,j párosra teljesül a feltétel:

%time for x in permutations(range(8)): if all([i==j or abs(i-j) != abs(x[i]-x[j]) for i in range(8) for j in range(8)]): print x

[0, 4, 7, 5, 2, 6, 1, 3]
[0, 5, 7, 2, 6, 3, 1, 4]
[0, 6, 3, 5, 7, 1, 4, 2]
[0, 6, 4, 7, 1, 3, 5, 2]
[1, 3, 5, 7, 2, 0, 6, 4]
[1, 4, 6, 0, 2, 7, 5, 3]
[1, 4, 6, 3, 0, 7, 5, 2]
[1, 5, 0, 6, 3, 7, 2, 4]
[1, 5, 7, 2, 0, 3, 6, 4]
[1, 6, 2, 5, 7, 4, 0, 3]
[1, 6, 4, 7, 0, 3, 5, 2]
[1, 7, 5, 0, 2, 4, 6, 3]
[2, 0, 6, 4, 7, 1, 3, 5]
[2, 4, 1, 7, 0, 6, 3, 5]
[2, 4, 1, 7, 5, 3, 6, 0]
[2, 4, 6, 0, 3, 1, 7, 5]
[2, 4, 7, 3, 0, 6, 1, 5]
[2, 5, 1, 4, 7, 0, 6, 3]
[2, 5, 1, 6, 0, 3, 7, 4]
[2, 5, 1, 6, 4, 0, 7, 3]
[2, 5, 3, 0, 7, 4, 6, 1]
[2, 5, 3, 1, 7, 4, 6, 0]
[2, 5, 7, 0, 3, 6, 4, 1]
[2, 5, 7, 0, 4, 6, 1, 3]
[2, 5, 7, 1, 3, 0, 6, 4]
[2, 6, 1, 7, 4, 0, 3, 5]
[2, 6, 1, 7, 5, 3, 0, 4]
[2, 7, 3, 6, 0, 5, 1, 4]
[3, 0, 4, 7, 1, 6, 2, 5]
[3, 0, 4, 7, 5, 2, 6, 1]
[3, 1, 4, 7, 5, 0, 2, 6]
[3, 1, 6, 2, 5, 7, 0, 4]
[3, 1, 6, 2, 5, 7, 4, 0]
[3, 1, 6, 4, 0, 7, 5, 2]
[3, 1, 7, 4, 6, 0, 2, 5]
[3, 1, 7, 5, 0, 2, 4, 6]
[3, 5, 0, 4, 1, 7, 2, 6]
[3, 5, 7, 1, 6, 0, 2, 4]
[3, 5, 7, 2, 0, 6, 4, 1]
[3, 6, 0, 7, 4, 1, 5, 2]
[3, 6, 2, 7, 1, 4, 0, 5]
[3, 6, 4, 1, 5, 0, 2, 7]
[3, 6, 4, 2, 0, 5, 7, 1]
[3, 7, 0, 2, 5, 1, 6, 4]
[3, 7, 0, 4, 6, 1, 5, 2]
[3, 7, 4, 2, 0, 6, 1, 5]
[4, 0, 3, 5, 7, 1, 6, 2]
[4, 0, 7, 3, 1, 6, 2, 5]
[4, 0, 7, 5, 2, 6, 1, 3]
[4, 1, 3, 5, 7, 2, 0, 6]
[4, 1, 3, 6, 2, 7, 5, 0]
[4, 1, 5, 0, 6, 3, 7, 2]
[4, 1, 7, 0, 3, 6, 2, 5]
[4, 2, 0, 5, 7, 1, 3, 6]
[4, 2, 0, 6, 1, 7, 5, 3]
[4, 2, 7, 3, 6, 0, 5, 1]
[4, 6, 0, 2, 7, 5, 3, 1]
[4, 6, 0, 3, 1, 7, 5, 2]
[4, 6, 1, 3, 7, 0, 2, 5]
[4, 6, 1, 5, 2, 0, 3, 7]
[4, 6, 1, 5, 2, 0, 7, 3]
[4, 6, 3, 0, 2, 7, 5, 1]
[4, 7, 3, 0, 2, 5, 1, 6]
[4, 7, 3, 0, 6, 1, 5, 2]
[5, 0, 4, 1, 7, 2, 6, 3]
[5, 1, 6, 0, 2, 4, 7, 3]
[5, 1, 6, 0, 3, 7, 4, 2]
[5, 2, 0, 6, 4, 7, 1, 3]
[5, 2, 0, 7, 3, 1, 6, 4]
[5, 2, 0, 7, 4, 1, 3, 6]
[5, 2, 4, 6, 0, 3, 1, 7]
[5, 2, 4, 7, 0, 3, 1, 6]
[5, 2, 6, 1, 3, 7, 0, 4]
[5, 2, 6, 1, 7, 4, 0, 3]
[5, 2, 6, 3, 0, 7, 1, 4]
[5, 3, 0, 4, 7, 1, 6, 2]
[5, 3, 1, 7, 4, 6, 0, 2]
[5, 3, 6, 0, 2, 4, 1, 7]
[5, 3, 6, 0, 7, 1, 4, 2]
[5, 7, 1, 3, 0, 6, 4, 2]
[6, 0, 2, 7, 5, 3, 1, 4]
[6, 1, 3, 0, 7, 4, 2, 5]
[6, 1, 5, 2, 0, 3, 7, 4]
[6, 2, 0, 5, 7, 4, 1, 3]
[6, 2, 7, 1, 4, 0, 5, 3]
[6, 3, 1, 4, 7, 0, 2, 5]
[6, 3, 1, 7, 5, 0, 2, 4]
[6, 4, 2, 0, 5, 7, 1, 3]
[7, 1, 3, 0, 6, 4, 2, 5]
[7, 1, 4, 2, 0, 6, 3, 5]
[7, 2, 0, 5, 1, 4, 6, 3]
[7, 3, 0, 2, 5, 1, 6, 4]
CPU time: 2.93 s,  Wall time: 3.00 s

for x in permutations(range(8)): if all([i==j or abs(i-j) != abs(x[i]-x[j]) for i in range(8) for j in range(8)]): show(matrix_plot([[ x[i]!=j for i in range(8)] for j in range(8)])) break

A következőkben egy négyzet alakú pályán megpróbálunk eljutni a start mezőről a cel mezőre. A szabály a következő: a négy szomszédos mezők valamelyikére léphetünk, ha ott nem X áll. (X jelképezi a falat.) Azt fogjuk megválaszolni, hogy mennyi a legrövidebb út start és cel között.

A pálya:

l=[['.','X','.','.'],['.','X','.','X'],['.','.','X','.'],['.','.','.','.']]

A join függvény egy szövegekből álló listát vár, eredményül a sztringek egymás után fűzését adja vissza. Második paraméterként megadhatjuk a szeparáló szöveget is, ami alapértelmezés szerint egy space.

join(['a','bb'])

'a bb'

join(['a','bb'],'')

'abb'

join(['a','b','cc'],'---')

'a---b---cc'

Szeretnénk a pályát jól ábrázolni, ebben lesz segítségünkre a kiir függvény. A későbbiekben szeretnénk meghívni olyan listával, amely tartalmaz számokat is, ezért nem print join(x) -szel írjuk ki az x sort, hanem str-rel átkonvertáljuk stringgé az összes elemet:

def kiir(l): for x in l: print join([str(y) for y in x])

kiir(l)

0 X . .
. X . X
. . X .
. . . .

A start koordináta (ez a [0,0] lesz) pozíciójába 0-t fogunk írni, mivel ez a mező 0 lépés után elérhető. A k értéke legyen 0, mivel eddig 0 a legnagyobb kitöltött számjegy.

A lépés legyen a következő: megkeressük az összes olyan mezőt, ahol '.' áll és van k-t tartalmazó szomszédja. Az ilyen mezőkre k+1-et írunk. Ezt valósítja meg a lepes(l,k) függvény.

Első lépésként készítünk a listánkból egy másolatot, mivel nem szeretnénk az l listát módosítani az algoritmus során.

def lepes(l,k): r=[x[:] for x in l] n=len(r) for i in range(n): for j in range(n): if r[i][j] == '.': if (i-1>=0 and r[i-1][j]==k) or (i+1<n and r[i+1][j]==k) or (j-1>=0 and r[i][j-1]==k) or (j+1<n and r[i][j+1]==k): r[i][j] = k+1 return r

Az előző függvényben egy érdekes dolog történt: (i+1<n and r[i+1][j] ==k) rész kiértékelésénél érvényesül a lusta kiértékelés. A python nem számol ki olyan dolgot, amit nem kell. Ha kíváncsi az A and B értékére, és kiszámolta, hogy A hamis, akkor nem fogja B-t kiszámolni (hiszen az értéke úgysem befolyásolna semmit). Itt is ezt használjuk: ha i+1<n nem teljesül, akkor r[i+1][j] ==k nem értékelődik ki (még jó, mert n. eleme az r listának már nem lenne, és hibát kapnánk).

l[0][0] értékét ideiglenes 0-ra állítjuk, hogy lássuk az algoritmus futásának eredményét:

l[0][0] = 0 kiir(lepes(l,0))

0 X . .
1 X . X
. . X .
. . . .

l értékét visszaállítom:

l=[['.','X','.','.'],['.','X','.','X'],['.','.','X','.'],['.','.','.','.']]

A következő folyam(s,start,cel) függvényben kiszámoljuk az l által meghatározott térképben start és cél távolságát. Először is készítünk s-ről egy másolatot l-be, majd beállítjuk a kezdő pozíciót 0-ra. Ezután addig iteráljuk a lepes függvényt, amíg különbözőt listát ad vissza. Ha már ugyanazt adja vissza, akkor a lépésekkel eljutottunk mindenhova. A kiir függvénnyel kiírjuk a végső pályát és visszaadjuk a cel által meghatározott helyen lévő elemet. Ez vagy az a szám, ahány lépésből elérhető a start pontból, vagy '.', ha nem elérhető.

def folyam(s,start,cel): l=[[ y for y in x] for x in s] l[start[0]][start[1]] = 0 k = 0 uj = lepes(l,k) while uj != l: l = uj k += 1 uj = lepes(l,k) kiir(uj) return l[cel[0]][cel[1]]

folyam(l,[0,0],[2,3])

0 X . .
1 X . X
2 3 X 7
3 4 5 6
7

Az önhasonló halmazokat meg lehet adni a hasonlóságukat meghatározó iterált függvényrendszerükkel, illetve minden kontraktív iterált függvényrendszerhez tartozik egy egyértelmű nem üres kompakt (most itt ezek korlátos és zárt) halmaz. A lényeg: tekintsük a következő 3 leképezést:

(x,y) -> (x/2,y/2)

(x,y) -> (x/2+1/2,y/2)

(x,y) -> (x/2,y/2+1/2)

A káosz játékot fogjuk játszani. Induljunk ki egy tetszőleges pontból, majd válasszunk véletlenszerűen a leképezések közül. A bejárt pontokat megjelenítjük.

def sier(p): c=randint(1,3) if c == 1: return [p[0]/2,p[1]/2] elif c==2: return [p[0]/2+1/2,p[1]/2] elif c==3: return [p[0]/2,p[1]/2+1/2]

def nestlist(f,x,n): r = [x] for i in [1..n]: x=f(x) r=r+[x] return r

list_plot(nestlist(sier,[0,0],10000),pointsize=1)

A véletlen "garantálja", hogy a fraktál így kirajzolódjon. Ha mindig az első függvényt választottuk volna, akkor nem kapnánk ilyen szép képet.

A Koch-görbe függvényrendszere már kicsit bonyolultabb. Az s változót előre definiálom (bár ilyet nem szoktunk csinálni) azért, hogy ne számolja ki minden egyes alkalommal a cos(pi/6) értékét. Azért használok n() függvényt, hogy lebegőpontos értékekkel számoljon végig.

s=cos(pi/6).n() def koch(p): c=randint(1,4) if c == 1: return [p[0]/3,p[1]/3] elif c==2: return [(p[0]/2-p[1]*s)/3+1/3,(p[1]/2+p[0]*s)/3] elif c==3: return [(p[0]/2+p[1]*s)/3+1/2,(p[1]/2-p[0]*s+s)/3] elif c==4: return [p[0]/3+2/3,p[1]/3]

list_plot(nestlist(koch,[0,0],10000),pointsize=1)