Utolsó módosítás: 2008. november 19.
Ezek a feladatok gyakorlásra szolgálnak, ezeket otthon vagy a konzultáción lehet megoldani. Némelyik feladat különálló, némelyik segíthet egy hasonló házi feladathoz. A feladatok egy részére megoldást is mutatok, egy részére nem raktam föl megoldást.
Az összes nyilvános példa bemenetet és kimenetet (a heti házi feladatokéval) egyben le lehet tölteni:
Egy bemeneti fájl minden sorában egy szó áll. Ezen szavaknak egy jelentős része p betűvel kezdődik. Szeretnénk megkeresni a fájl azon részeit, ahol hat vagy több egymás utáni sorban kis p betűvel kezdődő szó szerepel.
A következő program beolvassa a fájlt a standard bemenetről, megkeresi a legalább hat szó hosszú sorozatokat, és kiírja ezeket. A különböző sorozatok közé még egy üres sort is kiír.
Töltse le a programot. Fordítsa le a gcc -Wall -O -o s0f6 s0f6.c paranccsal. Töltse le az alábbi példa bemenetet is, majd próbálja ki a programot rajta a ./s0f6 < s0f6be0 paranccsal. A kapott kimenetet is letöltheti.
A program soronként olvassa be a bemenetet a standard bemenetről
az fgets függvénnyel.
A program akár hat sort is eltárol egyszerre a memóriában.
Amikor ugyanis öt p betűs sort beolvasott,
még nem tudhatjuk,
ezek részei-e egy legalább hat p betűs sorból álló sorozatnak.
Amíg a program nem olvasott be
hat egymás utáni p betűs sort,
addig a inseq változó hamis,
és a k változó adja meg,
hogy hány előző sor volt p betűs.
Ha bármikor beolvasunk egy nem p betűvel kezdődő sort,
akkor az előző sorok tartalmát eldobhatjuk,
és a két változót beállítjuk a kezdőértékre:
inseq hamis, k pedig 0 lesz.
Ha egy p betűs sort olvasunk,
akkor ezt a sort meghagyjuk a line tömb
k indexű elemében.
Amikor azonban beolvastuk a hatodik p betűs sort,
akkor először kiírjuk a hat eddig beolvasott sort a line
tömbből,
majd átváltunk a másik állapotba:
az inseq változó igaz lesz.
Ilyenkor már nincs szükség több sort eltárolni,
ezért k 0 lesz,
így csak a tömb nullás elemét használunk, azt is csak ideiglenesen,
egy sor feldolgozása közben.
Amikor az inseq igaz,
akkor nincs más dolgunk,
mint kiírni minden sort, amely p betűvel kezdődik,
de visszatérni a kezdőállapotba,
amint találunk egy másféle sort.
Ha a fájlnak vége,
akkor az fgets függvény null pointert ad vissza,
ilyenkor nincs több dolga a programnak,
tehát azonnal befejezi a ciklust.
Még egy turpisság van a programban:
az outbegin változó.
Ez igaz addig, amíg semmit sem írtunk ki,
később hamis.
Ezt felhasználva tudja a program egyszerűen megtenni,
hogy a különálló legalább hatos sorozatok között a program
kiír egy üres sort,
de az első sorozat előtt vagy az utolsó után semmit nem ír ki.
Miután alaposan megértette ennek a programnak a működését,
másolja le a forráskódot s0f1.c névre,
és a másolat módosításával próbálja megoldani
a 0. feladatsorból az 1. feladatot.
Háromszögszámnak hívjuk az k * (k + 1) / 2 = 1 + 2 + … + k alakú számokat, ahol k nemnegatív egész szám. Az első néhány háromszögszám tehát 0, 1, 3, 6, 10, 15, ….
Gauss bebizonyította, hogy minden természetes szám előáll három háromszögszám összegeként.
Feladat egy kis természetes szám ilyen előállításai közül megkeresni egy bizonyos előállítást, konkrétan a lexikografikus sorrend szerint utolsót.
Ha tehát n egy természetes szám, akkor az olyan (a, b, c) nemnegatív egészekből álló hármasok közül, ahol n = a * (a + 1) / 2 + b * (b + 1) / 2 + c * (c + 1) / 2, keressük azt, ahol a a lehető legnagyobb, és ha a legnegyobb a mellett is több számhármas is van, akkor b a lehető legnagyobb.
Például kis számokra a hármasok a következők.
n a b c 0 0 0 0 1 1 0 0 2 1 1 0 3 2 0 0 4 2 1 0 5 2 1 1 6 3 0 0 7 3 1 0 8 3 1 1 9 3 2 0 10 4 0 0 11 4 1 0 12 4 1 1 13 4 2 0 14 4 2 1 15 5 0 0 16 5 1 0 17 5 1 1 18 5 2 0 19 5 2 1 20 4 4 0
Írjon programot, ami a standard bemeneten egyetlen n természetes számot kap (meg egy újsor jelet; n < 10000), a kimeneten pedig kiírja a megfelelő a, b, c számokat.
Például ha a bemenet a következő,
4220
akkor a kimenet ez lesz:
91 7 3
mivel 4220 = 91 * (91 + 1) / 2 + 7 * (7 + 1) / 2 + 3 * (3 + 1) / 2; de 91-nél nagyobb a-val ugyanezt nem lehet elérni; és ha a = 91, akkor is csak b = 7 vagy b = 3 lehetséges, ezek közül pedig az első a nagyobb.
Egy másik be és kimenet letölthető innen.
Vizsgáljuk meg a következő programot, amely egy egyszerű labirintust állít elő.
Fordítsuk le a programot a gcc -Wall -O -o s0f8 s0f8.c paranncsal, majd futtassuk le a kapott s0f8 programot.
A program a kimenetre kirajzol egy négyszögrács alapú labirintust
(a kezdőpontot @, a célt > karakter jelöli).
Egy példa az s0f8ki0 fájlban látható.
A labirintus mindig megoldható, vagyis a kezdőponttól a célig el lehet jutni; azonban a labirintus általában elég unalmas, mivel túl kevés benne a fal (a példa még a jobbak közé tartozik).
A program úgy működik, hogy először a négyzetrácsba minden falat behúz, ezután addig rombol le véletlenszerűen egy-egy falak, amíg a kezdőpontból a célpontba el lehet jutni. A rombolás közben a program számon tartja, melyik szobákba lehet eljutni idáig a kezdőpontból. Amikor egy falat lerombolunk, megvizsgáljuk, hogy a fal két oldalán ugyanaz-e a helyzet. Ha már mindkét oldalra el lehet jutni, vagy még egyik oldalra sem, akkor nem csinálunk semmit. Ha az egyik oldalra már el lehet jutni, de a másikra még nem, akkor szélességi bejárást indítunk a faltól, hogy megkeressük az összes olyan szobát, ahova újonnan el lehet jutni.
A programnak a reach függvény a legérdekesebb része:
ez hajtja végre a szélességi keresést.
Ehhez egy pozíciókból álló sort használunk,
aminek a linequeue
és colqueue tömbök tárolják az elemeit,
a head az elejének az indexét adja meg,
a tail pedig a végéét.
A linequeue[tail] = l; colqueue[tail++] = c; utasítások
a sor végére beszúrják az (l,c) pontot;
míg az l = linequeue[head]; c = colqueue[head++]; utasítások
a sor elejéről eltávolítják az első pontot,
amely az (l,c) változókba kerül.
Gondoljuk meg, hogy ha ez utóbbi utasításpár helyett az
l = linequeue[--tail]; c = colqueue[tail]; utasításokat írnánk,
akkor a program továbbra is működne,
csak sor helyett vermet,
szélességi bejárás helyett mélységi bejárást végezne.
Megpróbálhatja megváltoztatni a printmap függvényt úgy,
hogy kirjazolja, melyik szobákat jelöltük meg a kezdőhelyzetből elérhetőnek.
Ha ezután a függvényt elég gyakran meghívja a többi eljárás közben,
láthatja, milyen sorrendben jelöli meg a program a szobákat.
Nehezebb feladatként megpróbálhatja megváltoztatni a programot úgy, hogy nem csak a kezdőhelyzetből elérhető pozíciókat követi nyomon, hanem teljesen számon tartja, hogy melyik cellából melyik másikba lehet eljutni. (Ilyen kis méretű labirintus esetén ez még könnyen megtehető, de ha sokkal nagyobb labirintust szeretne nagyon gyorsan előállítani, akkor már bonyolultabb algoritmust kell írnunk.) Ezután módosítsa a programot úgy, hogy egy falat csak 1/5 valószínűséggel rombol le, ha két olyan szobát választ el, amik között már más úton el lehet jutni. (Régebben írtam egy programot, ami ehhez a programhoz nagyon hasonló módon működik, de sokkal érdekesebb labirintusokat állít elő. A két program között valószínűleg ez a legfontosabb különbség, de más kisebb eltérések is vannak.)
Az (m, n) pozitív egész számokból álló számpárt barátságos számoknak nevezzük, ha m < n; n pozitív valódi osztóinak összege m; viszont m pozitív valódi osztóinak összege pedig n.
Például a legkisebb barátságos számpár a (220, 284). Ebben 220 pozitív valódi osztói az 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 100 számok, ezek összege 284; míg a 284 osztói az 1, 2, 4, 71, 142, amelyek összege 220.
Ennek a mintafeladatnak a célja, hogy megkeressük a legkisebb barátságos számpárokat.
Először gondoljuk át, hogy kell egy szám osztóinak az összegét kiszámolni. A leggyorsabban ezt úgy lehet megtenni, ha ismerjük a szám prímfelbontását. Így például 220 prímfelbontása 2^2 * 5 * 11, így a 220 pozitív osztói
1, 2, 2^2,
5, 5*2, 5*2^2,
11, 11*2, 11*2^2,
11*5, 11*5*2, 11*5*2^2.
A pozitív osztók összegét ez alapján fölírhatjuk szorzat alakban: (1 + 2 + 2^2) * (1 + 5) * (1 + 11) = 7 * 6 * 12 = 504. Csakhogy minket a pozitív valódi osztók összege érdekel, ezért ebből még le kell vonnunk az eredeti számot: 504 - 220 = 284.
Általában legyen az n pozitív egész szám prímtényezős felbontása
n = p_1^{α_1} * … * p_t^{α_t},
ahol minden p_i prímszám, és minden α_i kitevő pozitív egész. Ekkor könnyen beláthatjuk, hogy az n pozitív valódi osztóinak az összege
(1 + p_1 + … + p_1^{α_1}) * … * (1 + p_t + … + p_t^{α_t}) - n.
Ezek alapján a programot három részben fogjuk megírni. Először írunk egy programot, ami kiszámolja egy bemeneten adott szám prímfelbontását. Másodjára módosítjuk ezt a programot, hogy kiszámolja egy szám pozitív osztóinak összegét. Végül ezt felhasználva megírjuk a programot, ami barátságos számpárokat keres.
A prímfelbontást azzal az egyszerű módszerrel állítjuk elő, hogy sorra vizsgáljuk a 2, 3, 4, 5, … osztókat, és amelyikkel a szám osztható, azzal leosztjuk a lehető legtöbbször, majd kiírjuk az osztót és a kitevőt. Így, noha nem csak prímszámokkal próbálunk osztani, valójában csak prímosztókat fogunk találni, mert egy összetett számnak előzőleg az összes osztóját már eltávolítottuk a számból. Annyit gyorsítunk azonban a vizsgálaton, hogy az osztókat csak a szám négyzetgyökéig vizsgáljuk. Ezt megtehetjük, hiszen ha a számnak nincs a négyzetgyökénél kisebb vagy egyenlő prímosztója, akkor a szám prím.
Nézzük meg tehát a program első változatát, amely a standard bemeneten kapott szám prímfelbontását kiírja a standard kimenetre.
Változtatás: a fenti forráskódban volt egy hiba, egy fölösleges sor, amitől a forráskód nem is fordult le. Ezt november 19-én kijavítottam.
A main függvény meglehetősen egyszerű:
beolvas egy számot a bemenetről,
ellenőrzi (mivel a program maradék része csak 1-nél nagyobb pozitív számra működik helyesen),
és meghívja a decompose függvényt.
A decompose függvény végzi a tulajdonképpeni prímfelbontást.
Ebben a függvényben n a felbontandó egész,
a p változó fut végig az egészeken 2-től.
A pmax az n négyzetgyökét tárolja,
ha p ennél nagyobb, akkor már nincs remény arra,
hogy valódi osztót találjunk,
így p-t megnöveljük n-re.
A 0 == n % p feltétel akkor és csak akkor igaz,
ha n osztható p-vel.
Ha ez teljesül, akkor n-t elosztjuk p-vel.
Mivel egy prímosztó többszörösen is oszthatja n-et,
ezért ezt az osztást ciklusban végezzük.
Az akár többszöri osztás után a prímtényezőt
csak egyszer, kitevővel együtt írjuk ki;
és egyben ellenőrizzük, 1 == n igaz-e,
mert ekkor megvan a teljes prímfelbontás.
Fontos, hogy ha egyszer sem osztottunk, vagyis a kitevő nulla,
akkor ne írjunk ki semmit.
Fordítsuk le a programot a gcc -Wall -O -lm -o s0f9v0 s0f9v0.c paranccsal, futtassuk le a ./s0f9v0 paranccsal, és vigyünk be egy számot (például 28). Megkapjuk a prímfelbontást (például 2^2 * 7^1).
Most módosítsuk a programot úgy, hogy az osztók összegét számolja ki.
(A két forráskód közti különbségeket megtekinthetjük például a diff -u s0f9v0.c s0f9v1.c paranccsal.)
A decompose függvényt átneveztük sigma-ra,
és megváltoztattuk a típusát is,
mivel a függvény visszatérési értéke az osztók összege lesz.
Az új r változóba gyűjtjük az
(1 + p + … + p^α) értékek szorzatát
az eddig megtalált prímosztókra.
A kiíró utasítást tehát kicseréltük egy kódrészletre,
amely kiszámolja ezt az összeget,
és megszorozza r-et vele.
Végül a függvény végén található return utasítás
visszaadja a kapott r szorzatot.
Az, hogy a sigma függvény nem kiírja,
hanem visszatérési értéknek adja az osztók összegét,
a harmadik változatban lesz hasznos,
mivel ott az összeget nem kiírni fogjuk,
hanem további számításokra használjuk fel.
Az előzőhöz hasonlóan fordítsuk le a programot a gcc -Wall -O -lm -o s0f9v1 s0f9v1.c paranncsal, futtassuk a s0f9v1 parancsot például a 28 bemenetre, így megkapjuk, hogy a 28 pozitív osztóinak összege 56.
Végül nézzük meg a program utolsó módosítását is, amely már a barátságos számpárokat keresi.
Ez az előző sigma függvényt változatlanul használja,
csak a main függvény különbözik.
Ez egyszerűen megvizsgálja az összes n értéket
2-től kezdve, hogy barátságos szám-e.
Fordítsuk le ezt a programot is a gcc -Wall -O -lm -o s0f9v2 s0f9v2.c paranccsal, és kezdjük el futtatni a ./s0f9v2 paranncsal. (A program nagyon sokáig futna, ezért egy idő után állítsuk le a control-C billentyűkkel.)
Ebben a feladatban egy görbe alatti legnagyobb területű téglalap területét kell kiszámolni.
A bemenet egy sor áll, amely néhány nemnegatív egész számból áll szóközzel elválasztva, hívjuk ezeket A_0, &ellip; A_{N-1}-nek.
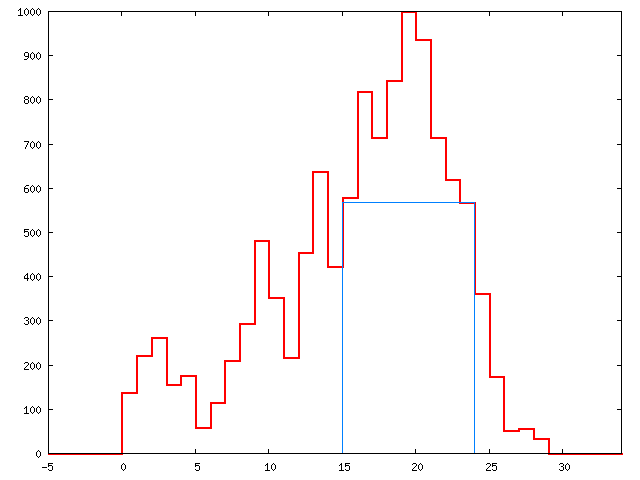
A számok egy függvénygörbét írnak le, ez a függvény K és K+1 között az A_K értéket veszi fel, ha 0 <= K < N egész; és nullát vesz fel a 0-nál kisebb és N-nél nagyobb helyeken. Az olyan téglalapok közül keressük a legnagyobb területűt, amelynek az egyik oldala az x tengyellyel párhuzamos, és teljes egészében a függvény grafikonja alatt, de az x tengely fölött fekszik.
Másképpen szólva a legnagyobb téglalap csúcsai biztosan (U, 0), (U, M), (V, M), (V, 0) ahol 0 <= U < V <= N egész számok, M egyenlő az A_U, &ellip; A_{V-1} számok közül a legnagyobbal. A téglalap területe (V - U)*M, ezt kell tehát maximalizálni.
Íme néhány példa.
A következő ábra az s0fabe0 bemenethez tartozik.

A feladat nehézsége abban rejlik, hogy a naív megoldás nagyon lassú. Van gyors megoldás is, ami a bemenet hosszában lineáris idő alatt végez, vagyis ez a leghosszabb példabemenetre is elég gyorsan lefut, de ezt egy kissé nehezebb megtalálni. Ettől függetlenül lassabb megoldást is érdemes lehet megírni, mivel ezzel ellenőrizhetjük a gyorsabb megoldás helyességét.